The act of comparing two numbers may seem like a trivial task if we do not think about it too much. From an early age, we know what is more, less, or equal when it comes to numbers. But what happens when we leave the world of pure, simple mathematics and enter our messy world with its variety of approximations and fuzziness? Quite often we end up with a notion of “close enough”.

Motivating Examples

Cruise Control

Consider, for example, a car with cruise control or an aeroplane with autopilot. In both cases, the user selects the desired speed, which we then want to maintain. We do not want to play with the controls all the time. Raising and lowering the power could result in overshooting and then undershooting, which would make the ride quite uncomfortable for our passengers.

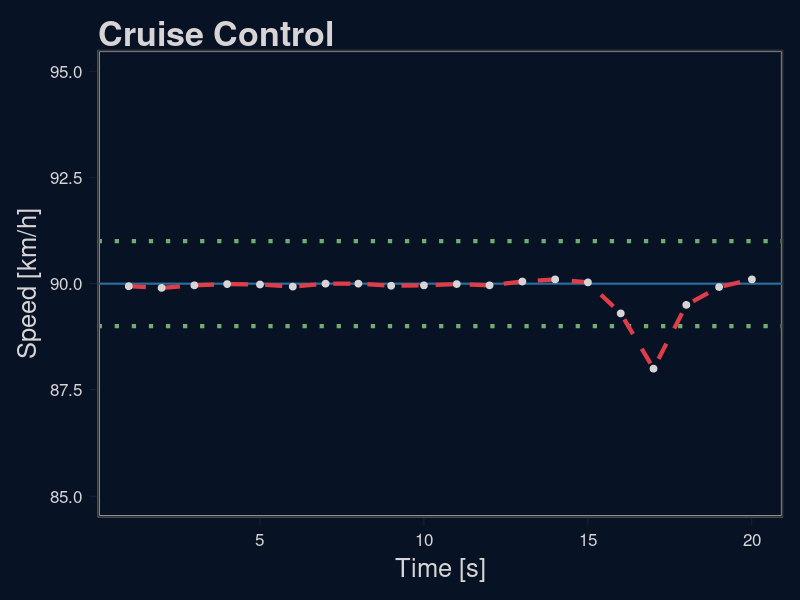
The most obvious solution is to define the “close enough” condition. As long as the speed is close enough to the target we do nothing. A road will have its bumps, wind can help or hurt a little, a passing truck will change the air movement around the car. As long as the measured speed is close enough to the target, we are fine. As soon as the speed slips out of our zone (for example, when the road starts to rise), we know we should start regulating.

Marubozu

In the financial markets, the most common way to represent price movements is to use candles. For any given time period, such as an hour or a day, we record the low, the high, the open, and the close. If the overall movement was positive and the close is above the opening price, the candle turns green. If the open is above the close and the price movement was negative, the candle turns red. The wicks at the top and bottom mark the highest and lowest price the asset had during that period.

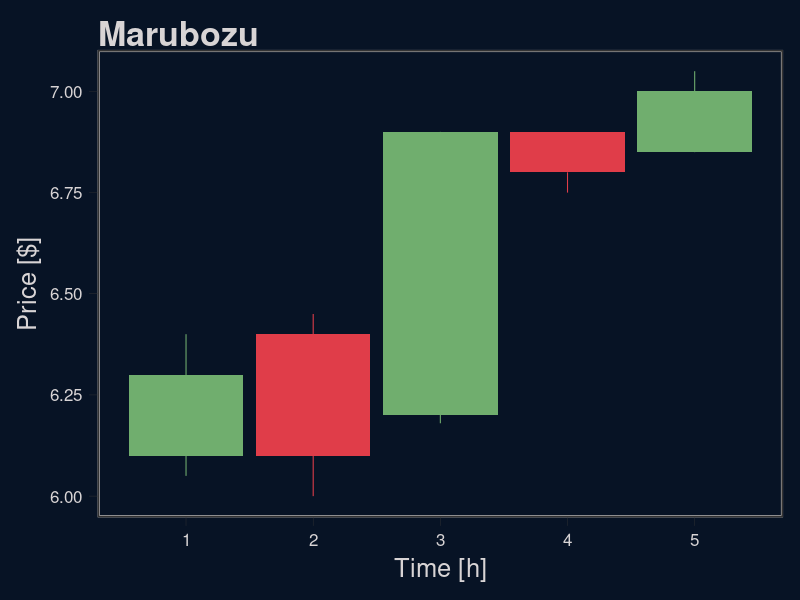
We can often use the shape of the candle to gain additional insight into the market. One of these shapes is called Marubozu. Red Marubozu has the open at its highest point and the close at its lowest. Green has the open at its lowest point and the close at its highest point. In summary, the Marubozu is a candle type that has no wicks. It only occurs in times of strong market direction, as the price goes more or less straight up or down without reversing at the extremes.

The best trades happen when the market has strong direction, so recognising Marubozus can be beneficial to a trading strategy. At this point, it’s important to remember that in real life, things are rarely perfect. We want a strategy that recognises Marubozu, even if it’s not quite perfect. We end up with the same idea of “close enough”.

Functions

None of the functions needed for this kind of tasks are complicated. But writing them over and over again still takes some brain power away from the task and is error prone. They are just complex enough for that. So let’s go through them one by one, write them down, and be done with it (at least for Rust).

Equal

For two numbers to be considered equal by our definition, they must be less than (or equal to) some margin apart. We could check this by subtracting one number from the other and checking that the absolute value of the result is less than the margin. Or we could check that one number is less than the other plus margin and greater than the same number minus margin, as we did below.

fn eq(lhs: f64, rhs: f64, margin: f64) -> bool
{
    (rhs <= (lhs + margin)) & (rhs >= (lhs - margin))
}

Not Equal

We could of course define not equal as negated equal. But since we want to get it right once, we can check whether one number is less than the other minus margin or greater than the other plus margin. So in essence, we are checking whether it is strictly greater or strictly smaller, which saves us an operation of negation.

fn ne(lhs: f64, rhs: f64, margin: f64) -> bool
{
    (lhs + margin < rhs) | (lhs - margin > rhs)
}

Greater Than

Greater than would be used to figure out when we need to decrease the power of a car in our first example. We simply check if the left side is greater than the right side plus margin.

pub fn gt(lhs: f64, rhs: f64, margin: f64) -> bool
{
    lhs > (rhs + margin)
}

Less Than

Less than simply reverses the equation. The left side should be smaller than the right side minus the margin.

pub fn lt(lhs: f64, rhs: f64, margin: f64) -> bool
{
    lhs < (rhs - margin)
}

Greater or Equal

Greater or equal could be translated as “at least”. The left side should be greater than or equal to the right side plus the margin.

pub fn ge(lhs: f64, rhs: f64, margin: f64) -> bool
{
    lhs >= (rhs - margin)
}

Less or Equal

Similarly, we could translate less or equal as “at most”. The left side should be less than or equal to the right side plus the margin.

pub fn le(lhs: f64, rhs: f64, margin: f64) -> bool
{
    lhs <= (rhs + margin)
}

FuzzyComp

Functions that deal with the same challenges as described above are collected in my crate called FuzzyComp. The added benefit is that a crate takes advantage of Rust’s extremely powerful generics to use functions with other data types, is properly tested and documented. These parts will be a topic of future blog posts.